Symplectic frame bundle

In symplectic geometry, the symplectic frame bundle[1] of a given symplectic manifold 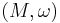(M, \omega)\, is the canonical principal 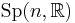{\mathrm {Sp}}(n,{\mathbb R})-subbundle 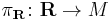\pi_{\mathbf R}\colon{\mathbf R}\to M\, of the tangent frame bundle 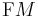\mathrm FM\, consisting of linear frames which are symplectic with respect to 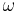\omega\,. In other words, an element of the symplectic frame bundle is a linear frame 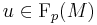u\in\mathrm{F}_{p}(M)\, at point 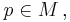p\in M\, , i.e. an ordered basis 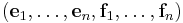({\mathbf e}_1,\dots,{\mathbf e}_n,{\mathbf f}_1,\dots,{\mathbf f}_n)\, of tangent vectors at 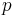p\, of the tangent vector space 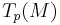T_{p}(M)\,, satisfying

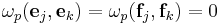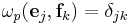
\omega_{p}({\mathbf e}_j,{\mathbf e}_k)=\omega_{p}({\mathbf f}_j,{\mathbf f}_k)=0\, and \omega_{p}({\mathbf e}_j,{\mathbf f}_k)=\delta_{jk}\,

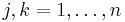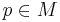for j,k=1,\dots,n\,. For p\in M\,, each fiber 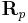{\mathbf R}_p\, of the principal 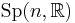{\mathrm {Sp}}(n,{\mathbb R})-bundle 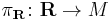\pi_{\mathbf R}\colon{\mathbf R}\to M\, is the set of all symplectic bases of T_{p}(M)\,.

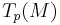The symplectic frame bundle 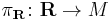\pi_{\mathbf R}\colon{\mathbf R}\to M\,, a subbundle of the tangent frame bundle 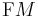\mathrm FM\,, is an example of reductive G-structure on the manifold M\,.

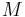See also

Notes

  1. ^ Habermann, Katharina; Habermann, Lutz (2006), Introduction to Symplectic Dirac Operators, Springer-Verlag, ISBN 978-3-540-33420-0  page 23

Books